最低限仲良くなりたい頻出な数式や統計量の行列表現 -

これ何

これまでなんとなく曖昧で避けてきてもなんとかなってきたけど、機械学習を勉強するに当たって当たり前のように出てくる数式や統計量の行列表現を当たり前の知識にする！

僭越ながら、機械学習を勉強すると、様々な理論が固有値問題や単純な確率統計が土台となることを痛感します。

逆にいうと、ベースを固めてしまえば、新しく学ぶ機械学習の理論もスムーズにインプットできると感じます。

まずは、数式の内容自体は簡単だけど見た目が記号になると慣れ親しんでないが故に一気に難しく感じる、ベクトルや行列表現の食わず嫌いを克服したい。

食べ物でいうとなんとなく崇高で見た目もまずそうだけど美味な「うに」を徐々に克服しようといったところ*1。

どんな人向け

例えば、3つの特徴量からなるデータがあった時、１つのサンプルデータ $\vec{x} = (x_1, x_2, x_3)$ を特徴量 $\vec{w} = (w_1, w_2, w_3)$ で重みづけして予測値yを表現するとするなら、

$y = w_1x_1 + w_2x_2 + w_3x_3$

と明示的に表現されればすんなり理解できるけど

より一般化して

$y = \boldsymbol{ w }^{\mathrm{T}} \boldsymbol{ x }$

と書かれるのは最初は「😇」となっちゃいがちな人*2。

はい、私もです。

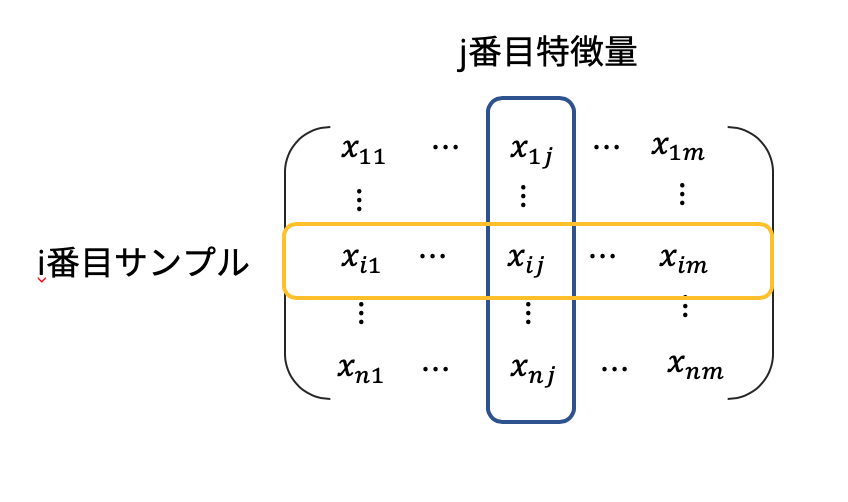
一般的なデータのまとめ方

これまで機械学習を学んできて、基本的には

1行が1サンプル
1列が1特徴量

が原則*3。そして、

特徴量=次元の数

である。
i番目のトレーニングサンプルのj個目の特徴量のデータは $x_{ij}$ と表現される。

f:id:wimper_1996:20200122011442p:plain:w380
太字のアルファベット $x$ は通常[列ベクトル]を表すと言っていい。
つまりj個目の特徴量を表す列ベクトル $x_j$ (j次元, j変量とも言う)は

$\boldsymbol{ x }_j = \left( \begin{array}{c} x_{1j} \\ x_{2j} \\ \vdots \\ x_{nj} \end{array}\right) = (x_{1j}, x_{2j}, \ldots, x_{nj})^{\mathrm{ T }}$

となる。ここまでは、基本の基本。

行列計算で意識してほしいこと

機械学習においてnumpyを使った行列計算は頻出。

import numpy as np
a = np.dot(b, c)

これは、行列積 $A = BC$ を表す。

このような行列計算を行う際、必ず意識してほしいこと。

行列の行と列の数をチェックする

行列積の計算では、必ず、各要素の外側の行と列が残る。どういうことかというと
f:id:wimper_1996:20200123024757p:plain

例えば
$\displaystyle \begin{pmatrix} 1 & 2 & 3 \\ 3 & 4 & 5\end{pmatrix} \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array}\right)$
という(2×3)と(3×1)の行列積を考えてみると、答えは $\left( \begin{array}{c} 6 \\ 12 \end{array}\right)$ となり、(2×1)となることがわかる。行列積では、内側の数(今回の場合3)は必ず等しい。

そして、残るのは、１つ目の行列の「行」と、最後の行列の「列」だけである。

色々な行列同士の掛け算を見たとき、まず行と列の掛け算をチェックしてみてください。

それを意識するだけで正しい行列演算にたどり着くことも多く、理解の幅が広がります。

それでは、具体的な式をいくつか見ていきます。

線型結合

冒頭でも触れた例。
m個の重みベクトル $\boldsymbol{ w }$ とデータの入力ベクトル $\boldsymbol{ x }$ を用いて表される予測値 $y$ は、式で書くと

$\displaystyle y = w_1x_1 + w_2x_2 + ... + w_mx_m$

これを行列で表すと、wとxが両方とも縦ベクトルの場合、

$\displaystyle y = \boldsymbol{ w }^{ \mathrm{ T } } \boldsymbol{x}$

となる。w(またはx)どちらかを転置することがすぐわかるようにしましょう。

pythonで書くと

np.dot(w.T, x)

wとxが両方縦ベクトルの場合, そのままだと(m, 1)と(m,1)の行列演算はできないので片方を転置します。

もし自分で行列の形を設定するとき、wを横ベクトルと考えた場合は $\displaystyle y = \boldsymbol{ w } \boldsymbol{x}$ という式になり、

np.dot(w, x)

でOK.

また、これはベクトル $\vec{x}$ からベクトル $\vec{w}$ への射影、すなわち内積を表しているともいえる。

$\displaystyle y = \boldsymbol{ w }^{ \mathrm{ T } } \boldsymbol{x} = w_1x_1 + w_2x_2 + ... + w_mx_m = (\boldsymbol{ w }, \boldsymbol{ x })$

分散(variance)と共分散(covariance)

j個目の特徴量の偏差平方和は、j特徴量における平均 $\mu$ を用いて $\displaystyle \sum_{ i = 1 }^{ n } (x_{ij} - \mu_{j})^2$ と表される。
j個目の特徴量の(不偏)分散 $\displaystyle x_j$ は、偏差平方和を(データ数-1)で割った値である。

$\displaystyle v = s_{jj} = \frac{1}{n-1} \sum_{ i = 1 }^{ n } (x_{ij} - \mu_{j})^2$

共分散は、ある1つのサンプルにおける、2つの特徴量jとkの分散にあたり、 $x_j$ と $x_k$ の偏差積和をn-1で割ったもの。式で書くと

$\displaystyle s_{jk} = \frac{1}{n-1} \sum_{ i = 1 }^{ n } (x_{ij} - \mu_{j})(x_{ik} - \mu_{k})$

これを行列で書く(一般化する)と

$\displaystyle \frac{( X^{ \mathrm{T} } - \mu)(X - \mu)}{n-1}$

となる。各データを正規化(平均をゼロ)して、

$\displaystyle S = \frac{X^ \mathrm{T} X}{ n-1 }$

と書かれることが多い。pythonで書くと

# X.shape = (n_samples, m) であるとする
# 正規化して, 共分散行列を求める
u = np.mean(X, axis=0)
n_samples = X.shape[0]

S = np.dot((X - u).T, (X - u)) / (X_train.shape[0])

# あるいはこれで一発
np.cov(X)

この行列の形は何x何でしょうか？

答えは、(mxm)で、特徴量x特徴量の対角行列です(下図)。
対角成分が分散、右上(左下)が共分散となります。

全生徒の、身長, 体重, 靴のサイズ....といった変数の関係性が見たいと考えるとわかりやすいでしょうか。

f:id:wimper_1996:20200122231544p:plain

相関係数

例えばXとYの共分散は、「(Xの偏差) ×(Yの偏差)」の平均であり、２変数間のばらつきを表す指標と言える。

ただ、これだとスケールに依存するという問題がある。例えばXが数学でYが国語の点数である場合、満点が10点か100点かによって値がかなり変わってくる。

共分散をスケール化したものが、相関係数であり、式で表すと

$\displaystyle r_{jk} = \frac{ s_{ jk } }{\sqrt{ s_{ ii } } \sqrt{ s_{ jj } } }$

つまり、共分散を、分散の平方根(=標準偏差)で割ったものである。これを行列で表すと

$\displaystyle R = \frac{X^ \mathrm{T} X}{ \sigma_{i} \sigma_{j} }$

ここで、 $\sigma_{i}$ は標準偏差を表す(= $\sqrt{s_{ii}}$ )。

pythonで書くと

np.corrcoef(X)

固有値問題

これも基礎知識としておくべき事項。
普通、とあるベクトル $\vec{v}$ に行列 $A$ をかけると、回転して向きが変わる。例えば
$\displaystyle \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \left( \begin{array}{c} 1 \\ 1 \end{array}\right) = \left( \begin{array}{c} 3 \\ 7 \end{array}\right)$
となるが、これは $\vec{v} = \left( \begin{array}{c} 1 \\ 1 \end{array}\right)$ というベクトルが、 $\vec{v}' = \left( \begin{array}{c} 3 \\ 7 \end{array}\right)$ というベクトルに回転＆拡大したと見なせる。

しかし、稀に、行列をかけても回転せず大きさだけが変わるベクトルが存在する。このベクトルが固有ベクトル(eigen vector)であり、変化した大きさを表すのが、固有値(eigen value)である。式で書くと

$\displaystyle A\vec{v} = \lambda\vec{v}$

求め方も一応備忘録として。まず上記の式の右辺を左辺に移行すると

$\displaystyle (A-\lambda E) \vec{v} = \vec{0}$

Eは単位行列。もし $A-\lambda E$ 部分が正則(non-singular matrix / regular matrix)であるとするなら(逆行列を持つなら)、 $\vec{v}$ が0でなければならない。

逆に言うと、 $\vec{v}$ が解をもつ条件は、正則でなくなる条件式、

$\displaystyle \begin{vmatrix} A-\lambda E \end{vmatrix}=0$

を満たせば良い。これが固有方程式と呼ばれるもので、これを解く問題を固有値問題という。
具体的な解き方は教科書などを参照してほしい。

ただ、機械学習において固有値問題を解くときは、numpyのパッケージを用いて

np.linalg.eig(A)

で一発で求まるので、解き方に固執する必要はない。

さて、固有ベクトルを横に並べた行ベクトル $V = ( \vec{v_1}, \vec{v_2} \ldots)$ と、それに対応するように固有値を対角上に並べた対角行列 $\varLambda = \begin{eqnarray}\left( \begin{array}{ccc} \lambda_1 & 0 & \ldots \\ 0 & \lambda_2 & \dots \\ \vdots & 0 & \ldots \end{array}\right)\end{eqnarray}$ を用いて、行列表現を書くとこうなる

$\displaystyle AV = V\varLambda$

ベクトルで書いた式と見比べて、 $V$ と $\varLambda$ の順番が違うことに注意。
Aの右から逆行列 $V^{-1}$ をかけて $A = V\varLambda V^{-1}$ となる。

この時、固有ベクトル同士は独立であり、正規直交基底をなす。つまりVは直交行列である。よって $V^{-1} = V^{\mathrm{T} }$ であることを用いて

$\displaystyle A = V\varLambda V^{\mathrm{T}}$

これを、「Aの固有値分解」あるいは「対角化」という。

必ず、正方行列(n×n)＝正則行列(n×n)・対角行列(n×n)・正則行列(n×n)の形になる。

何が嬉しいの

2つある。

1つ目。嬉しいというか、必要です。

機械学習の理論でバンバン出てきます。
主成分分析(Principal Component AnalysisPCA)や、特異値分解(Singular Value Decomposition: SVD: )、線形判別分析(Linear Discriminant Analysis: LDA)といった「次元圧縮」は、この固有値分解がベースといってもいい。

固有値分解の形は必ず理解しよう。

2つ目。少し蛇足かもしれないが、もともと対角化は、 $A^{n}$ を求めるために編み出されたもの*4らしい。
なぜかというと
$\displaystyle A^{n} = (V\varLambda V^{-1})^{n} = (V\varLambda V^{-1})(V\varLambda V^{-1}).... = V\varLambda^{n} V^{-1}$ が成り立つから。( $VV^{-1} = 1$ で全て打ち消される)

$\varLambda = \begin{eqnarray}\left( \begin{array}{ccc} \lambda_1^{n} & 0 & \ldots \\ 0 & \lambda_2^{n} & \dots \\ \vdots & 0 & \ldots \end{array}\right)\end{eqnarray}$

を見ると、対角成分以外は全てゼロだし、行列Aをn回掛け算するよりもいかにも簡単に求まって嬉しそう。

対角化もろもろについてはこのブログが詳しいのでぜひ。
kriver-1.hatenablog.com

その他呼吸するがごとく当たり前にしたい数式や記号など

$\| w \| = \sqrt{w_1^{2} + w_2^{2} + ... }$

ノルム：ベクトルの重みの二乗和の平方根(つまり大きさ)
これを行列で表すと

(発展) $\| A \|_F = \sqrt{ \sum_{ i,j }^{ m,n } a_{ij} }$

Frobeniusノルムといい、全成分の二乗和の平方根である。Fの添字がつくことが多い。

pythonでは

np.norm(x)

(ここまで見たように、数値演算では関数が実装されていることが多いnumpyを活用しまくります。)

$\boldsymbol X \in \mathbb{ R }^{n×m}$

n×m次元 = n個のデータとm個の特徴量からなる実数空間に属するX。

合成関数の微分 $\frac{ \partial f(z) }{ \partial z }$ の求め方

シグモイド関数 $a = \sigma(z) = \frac{ 1 }{ 1 + e^{-z} }$
この導関数 $\frac{ \partial a }{ \partial z }$ の結果をaを用いて表すとどうなるでしょうか？
スラスラ算出できるようにしましょう*5。
ちなみに、シグモイド関数はnumpyには実装されていないので自分で書く必要があります。

def sigmoid(x):
     a = 1 / 1 + np.exp(-x)
     return a

合成関数の微分(またの名を連鎖律)は、単回帰分析における重みの算出(最小二乗法)、からニューラルネットワークまで、あらゆるところで出てきます。超超頻出です。

これ以外にも色々ある気がしますが力尽きてきたので、また今後、追記する可能性ありです。

混乱しがちな行列表現の定義と英語表現

正則行列: regular matrix , non-singular matrix(非特異行列), inversible matrix (可逆行列)

逆行列をもつ行列のこと。 $AB = BA = E$
を満たすn次正方行列Bが存在するとき、BをAの逆行列といい、Aは正則であるという。
すごく覚えにくいが、英語でいろんな言い回しがされているので、わかるようにした方が良さそう。

私なりの覚え方↓
regular = 等辺等角 → 数学でいう正多角形の「正」の部分を表す
inversible = 逆にできる → 逆行列が存在する。
non-singular = 非特異値 → なんか0が多くなさそうだから逆行列持ちそう(適当)

転置行列: transpose

$A^{\mathrm{T}} = A$ となるような正方行列A

直交行列: orthogonal matrix

$A^{ \mathrm{T} }A = AA^{ \mathrm{T} } = E, すなわち A^{ \mathrm{T} } = A^{-1}$ となるような正方行列A

(補足) エルミート行列 $A^{\dagger}$ : hermitian matrix

定義は $A^{\dagger} = A$
ある行列Aの複素共役(複素部分の符号を反対にすればいい)をとり、さらに転置させた $A^{\dagger}$ が元の行列Aに等しいということ。
つまり、「対称行列」をさらに複素数の行列に対して一般化したもの。

(補足) ユニタリー行列 $A^{*}$ : unitary matrix

定義は $U^{*}U = 1$
これは、「直交行列」をさらに複素数の行列に対して一般化したもの。

以下定義省略で英単語リスト

逆行列: inverse matrix
対角行列: diagonal matrix
固有ベクトル/ 固有値: eigen vectors/ eigen values

最後に

深夜に思いつく限りのことを書き出しました*6。
私自身、機械学習という底無し沼にしばしば絶望感を覚えつつも、あ〜〜色々分かって繋がって楽し〜〜と思いながら勉強しています。楽しむのが一番です。

至らないところが多々ありますが、初心者視点の本記事が次に勉強する人たちの少しでも役に立てますように。

間違っている箇所があったら指摘していただけると幸いです。

参考文献

1. 奥村吉孝, 手嶋忠之(2012), 基礎から学び考える力をつける線形代数
2. 長畑秀和(2001), 多変量解析へのステップ
3. [第2版]達人データサイエンティストによる理論と実践 Python 機械学習プログラミング

*1:まだ全然好きじゃない

*2:特に研究室所属したての後輩とかに見てもらいたい…

*3:最近Courseraの大人気Andrew Ng先生のコースでニューラルネットワークを学んでいるが、深層学習の研究分野では各データが1列で表記されるのが一般的らしく、絶賛混乱している。ので、行と列が何を表しているのか常に意識するの超大事。

*4:参考文献1より

*5:a(1-a)になります

*6:めっちゃ時間かかった割に読み返してみるとあんまり内容がない......