2020-06-10

#BlackLivesMatterとつぶやくのではなくて

雑記

日本では最近，

緊急事態宣言が解除されたーとか，

また新型コロナウイルスの第二波が来そうだぞーとか，

そういった報道が大半を占めているわけだけども，

一方海を超えたアメリカでは，１０万人以上の死者を輩出している新型コロナウイルスの話題が脇に追いやられ，

一人の黒人男性の死がアメリカ全土に渡り抗議運動を呼び起こしている．

無抵抗のジョージフロイドさんが，「I can't breath」と言っている中，約9分に渡り膝で首を押さえられて窒息死した事件。

言葉通り

対岸の火事

報道が少ないし，あまり注目されていないように思う．

単純に，周りに黒人が少なく，当事者意識を持ちにくいからだろう．

確かにこの問題だけ見れば，自分とはほとんど関係がないように思える．

ただ，差別という問題は日本でも全く人ごとではない．

一番メジャーなのは女性の立場の低さといったところか．

www.nikkei.com

国際労働機関によると，2018年に世界の管理職に占める割合の平均は27.1%

アメリカが39％で最も多く，

最も低いのはアラブ諸国で11.1％

さて日本は？？

12％

いや最下位とほとんど変わらないやんけ。もちろんG7の中で最下位。

すっくねえ。アメリカすげえ。管理職の４割が女性か。

いいなあ。

「黒人だから危険だ」

「女性だから役員の地位はそぐわない」

両者は紙一重の問題だ．

黒人の方々の差別の辛さは当人にしか絶対にわからない．

「黒人」という外見を有するだけでバイアスがかけられてきた経験なんて，本人にしか辛さがわからない．

アメリカ建国時から存在していた奴隷制度に根付く，構造的な問題なのだ．

BBCの記事よりいくつかの興味深いデータを． f:id:wimper_1996:20200609230723p:plain

アフリカ系アメリカ人は人口の１３％しかいないのに，2019年警官から撃たれて死亡してしまう人の割合は２３％を占めている．

f:id:wimper_1996:20200609231056p:plain

100,000人当たりで見ると，アフリカ系アメリカ人の方が５倍近く白人よりも実刑判決を受ける．

これは衝撃。

「もし自分が黒人に生まれていたら」

偽善者みたいなセリフかもしれないけど

自分が何人に生まれていたかなんてサイコロの確率でしかない．

黒人の人々は，幼少期から警察とどう向き合うか，また社会でどう振る舞うか教育されるらしい．

自分は危害人物ではないと示すために．

www.huffingtonpost.jp

これをきっかけで，急に「人種差別反対！」と声高く偽善者ぶるつもりもない．

ただ，アメリカにいる黒人の人々が少しでも平等に，

歴史が転換されるように，私が少しでもできることをしたいと思った。

単にハッシュタグで#BlackLivesMatterと呟いたり，

Instagramで黒い画像を載せるのではなく。

という訳でこれに参加した。

youtu.be

広告収入の100％が，抗議者の保釈金や遺族の葬儀支援金として動画冒頭に掲げられている支援団体に寄付されるらしい．

6月9日時点で1000万再生，１０万コメント．

それなりに信頼性があると感じた．

動画自体の長さは1時間で，広告を中断せずに流す必要がある．

動画自体は様々なミュージシャンやアーティストなどが音楽や自信の気持ちを発信する内容となっている．

流石に長すぎるので，私は数分してからiPadで無音再生させ続けた．

微力であることは百も承知，

でも知らないことより向き合うこと，ハッシュタグで呟くより行動すること．

金銭的な支援ができるならなおさら．

ちなみに，ホワイトハウスへの抗議署名は40万以上に登り，目標を達成しているらしい．

それでも，SNSへの投稿2800万に比べたら，署名数は大いしたことがない．

「黒塗りの画像」の投稿以外に、あなたは黒人の権利のために何をしただろうか？ | Vogue Japan

ちっぽけな人間に過ぎないけど，支援するならせめて意味のあることをやっていこうかと思った．

そして何より

誰に対しても尊重心を持って接すること

小並感....

でもこれがめちゃくちゃ難しいんだよなあ．

どうしても自分基準で接すると，

「え，これは当たり前だよね？」「私でもできるんだからあなたも当然....」

のような態度を取ってしまうことがある...

これも偏見の一種。

色々努力していかないといけない。

最後にこちらの記事の紹介．

「Black Lives Matter」へ「いや黒人だけじゃなくて全ての命が大切だろ！」のような批判に対して。

なぜ「All Lives Matter（すべての命が大切）」と言うのをやめる必要があるのか｜ハーパーズバザー（Harper's BAZAAR）公式

アメリカの著名歌手ビリーアイリッシュさんはインスタにて納得の例え

もし友達が腕を怪我したら，"すべての腕は大切だから"って誰かがその友達にバンドエイドをあげるのを待ってるの？違うよね．友達を助けるよね，だってその友達は痛がってて，今助けを求めているから

要は，「黒人の命も大切だ」と言ってるからって白人を今度は排他的に考えている訳ではないよってこと。

f:id:wimper_1996:20200610001026j:plain

Black Lives Matter

想像以上に深い。

この記事が少しでもBlack Lives Matterの問題を知ったり，

自分ごととして考えたり，

あわよくば行動しようかなと思ってくれるきっかけになってくれたらそんな嬉しいことはないです。

2020-06-08

はじめてのUbuntu Docker導入 [七転八倒記]

Docker

これ何

Ubutu何？状態の人間がUbuntuでDocker環境を構築し機械学習を行うまでの備忘録

2020年5月時点での公式ドキュメント

matsuand.github.io

かなり丁寧です

必要なもの
https://github.com/NVIDIA/nvidia-docker/wiki/Installation-(Native-GPU-Support)

(当たり前) GNU/Linux x86_64 with kernel version > 3.10：LinuxのOS
(当たり前) NVIDIA GPU with Architecture > Fermi (2.1): つまりGPUデバイスそのもの
NVIDIA drivers ~= 361.93 (untested on older versions): NVIDIA® GPU ドライバ
Docker >= 19.03
NVIDIA Container Toolkit: DockerのNVIDIA® GPU サポート．DockerとNVIDIAのドライバーがインストールされていることが必要．

手順

目標：研究室にあるGPU付きのUbuntuデスクトップに，Docker環境を構築してGPUを接続し，Jupyter Notebook上で動きを確認する

現状の確認
Dockerをインストール
nvidia-container-toolkitのインストール
Dockerを起動

なぜDockerか

地道な環境構築で必要なもの

NVIDIA製のGPU
NIVIDA Driver
CUDA: GPUアプリケーション開発環境 (低レベルなプログラミング言語の実行環境) を提供する
cuDNN：DNN のためのプリミティブな GPU-accelerated library
TensorFlow（GPU版）
Keras

地道にGPUを認識するには，ensorflow, Cuda, cuDNNの各バージョンを全て合わせる必要がある。基本的に、tensorflowのバージョンを最初に決めたあと、その他のバージョンを決定する．

https://www.tensorflow.org/install/source#tested_build_configurations

Dockerを使うことでドライバしか必要ないため，互換性を考えなくて済むのが魅力的....

現状，インターネット上での情報はまだまだ上記のやり方が多くて，互換性に苦労している話が多い．

そう，何を隠そう私もそれで挫折した者の1人なので，潔くDockerに乗り換えることにした次第です．

Tensorflow公式サイトより

Docker を使用すると、ホストマシンに必要なのは NVIDIA® GPU ドライバだけになるので、GPU 上で TensorFlow を実行する際の最も簡単な方法となります（NVIDIA® CUDA® ツールキットは不要です）。

DockerでGPUサポートを使うには，追加でNVIDIA Container Toolkit をインストールする必要がある．

現状の確認

Dockerを導入するにはUbuntuは以下のいずれか，64-bitのバージョンであることが必要

Ubuntu Eoan 19.10
Ubuntu Bionic 18.04 (LTS)
Ubuntu Xenial 16.04 (LTS)

# ubuntuのバージョン確認
$ cat /etc/os-release

NAME="Ubuntu"
VERSION="18.04.4 LTS (Bionic Beaver)"
ID=ubuntu
ID_LIKE=debian
PRETTY_NAME="Ubuntu 18.04.4 LTS"
VERSION_ID="18.04"
HOME_URL="https://www.ubuntu.com/"
SUPPORT_URL="https://help.ubuntu.com/"
BUG_REPORT_URL="https://bugs.launchpad.net/ubuntu/"
PRIVACY_POLICY_URL="https://www.ubuntu.com/legal/terms-and-policies/privacy-policy"
VERSION_CODENAME=bionic
UBUNTU_CODENAME=bionic

# グラフィックボードとドライバーの確認
$ nvidia-smi
Fri May 15 01:18:25 2020       
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 440.64.00    Driver Version: 440.64.00    CUDA Version: 10.2     |
|-------------------------------+----------------------+----------------------+
| GPU  Name        Persistence-M| Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp  Perf  Pwr:Usage/Cap|         Memory-Usage | GPU-Util  Compute M. |
|===============================+======================+======================|
|   0  GeForce GTX 108...  On   | 00000000:18:00.0 Off |                  N/A |
| 29%   30C    P8     8W / 250W |      1MiB / 11178MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+
|   1  GeForce GTX 108...  On   | 00000000:3B:00.0 Off |                  N/A |
| 29%   31C    P8     9W / 250W |      1MiB / 11178MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+
|   2  GeForce GTX 108...  On   | 00000000:86:00.0 Off |                  N/A |
| 20%   31C    P8     8W / 250W |      1MiB / 11178MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+
|   3  GeForce GTX 108...  On   | 00000000:AF:00.0 Off |                  N/A |
| 29%   32C    P8     8W / 250W |      1MiB / 11178MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+
                                                                               
+-----------------------------------------------------------------------------+
| Processes:                                                       GPU Memory |
|  GPU       PID   Type   Process name                             Usage      |
|=============================================================================|
|  No running processes found                                                 |
+-----------------------------------------------------------------------------+

Ubuntuデスクトップのバージョンは18.04で，
[GeForce GTX 1080 Ti]が４つ搭載されている．また，既にGPUのドライバーとCUDA Toolkit (バージョンは440) も一式インストールされている．

もしドライバーがなかった場合

コマンドラインで最適なドライバを検索
公式サイトで確認する

2通りの方法がある．

$ ubuntu-drivers devices

== /sys/devices/pci0000:3a/0000:3a:00.0/0000:3b:00.0 ==
modalias : pci:v000010DEd00001B06sv00001043sd000085E5bc03sc00i00
vendor   : NVIDIA Corporation
model    : GP102 [GeForce GTX 1080 Ti]
driver   : nvidia-driver-415 - third-party free
driver   : nvidia-driver-410 - third-party free
driver   : nvidia-driver-435 - distro non-free
driver   : nvidia-driver-390 - distro non-free
driver   : nvidia-driver-418 - third-party free
driver   : nvidia-driver-440 - third-party free recommended
driver   : xserver-xorg-video-nouveau - distro free builtin

recommendedと記載されているやつをダウンロードする

でも，公式サイトだと f:id:wimper_1996:20200608050053p:plain f:id:wimper_1996:20200608050104p:plain

バージョン430がヒットした。440だとあまり情報がなかったので430のほうが良いかもしれない...

$ sudo apt-get install nvidia-driver-430

Dockerのインストール

HTTP経由で必要なパッケージをインストールする

# sudoは管理者権限でコマンドを実行するという意味

$ sudo apt-get update

$ sudo apt-get install \
    apt-transport-https \
    ca-certificates \
    curl \
    gnupg-agent \
    software-properties-common

Dockerの公式GPG keyを追加

$ curl -fsSL https://download.docker.com/linux/ubuntu/gpg | sudo apt-key add -

OK

鍵を取得し、fingerprintが9DC8 5822 9FC7 DD38 854A E2D8 8D81 803C 0EBF CD88であることを確認最後の８文字0EBFCD88が一致していることを確認

$ sudo apt-key fingerprint 0EBFCD88
pub   rsa4096 2017-02-22 [SCEA]
      9DC8 5822 9FC7 DD38 854A  E2D8 8D81 803C 0EBF CD88
uid           [  不明  ] Docker Release (CE deb) <docker@docker.com>
sub   rsa4096 2017-02-22 [S]

安定版(stable)リポジトリをセットアップする Ubuntuのアーキテクチャを確認し、HPで対応するリポジトリのコマンドをコピーする

$ uname -a

Linux okadaken 5.3.0-51-generic #44~18.04.2-Ubuntu SMP Thu Apr 23 14:27:18 UTC 2020 x86_64 x86_64 x86_64 GNU/Linux

f:id:wimper_1996:20200608050606p:plain

x86_64とは？amd64の別名．
amd64とは？x86を64ビットに拡張したx64対応のもの
armhfとは？ARMというCPUアーキテクチャ上で動かす、浮動小数点数命令を使うバージョン。Raspberry Piなどがこちらを使います。*1

つまり今回はx86_64 / amd64の部分のコマンドを選択すれば良い

そのままコピペ

$ sudo add-apt-repository \
   "deb [arch=amd64] https://download.docker.com/linux/ubuntu \
   $(lsb_release -cs) \
   stable"

DOCKER ENGINEのインストール
Dockerとcontainerdの最新版をインストール

$ sudo apt-get update
$ sudo apt-get install docker-ce docker-ce-cli containerd.io

Dockerコンテナの動作確認

$ sudo docker run hello-world

Unable to find image 'hello-world:latest' locally
latest: Pulling from library/hello-world
0e03bdcc26d7: Pull complete 
Digest: sha256:6a65f928fb91fcfbc963f7aa6d57c8eeb426ad9a20c7ee045538ef34847f44f1
Status: Downloaded newer image for hello-world:latest



Hello from Docker!
This message shows that your installation appears to be working correctly.



To generate this message, Docker took the following steps:
 1. The Docker client contacted the Docker daemon.
 2. The Docker daemon pulled the "hello-world" image from the Docker Hub.
    (amd64)
 3. The Docker daemon created a new container from that image which runs the
    executable that produces the output you are currently reading.
 4. The Docker daemon streamed that output to the Docker client, which sent it
    to your terminal.



To try something more ambitious, you can run an Ubuntu container with:
 $ docker run -it ubuntu bash



Share images, automate workflows, and more with a free Docker ID:
 https://hub.docker.com/



For more examples and ideas, visit:
https://docs.docker.com/get-started/

nvidia-container-toolkitのインストール

# Add the package repositories
$ distribution=$(. /etc/os-release;echo $ID$VERSION_ID)
$ curl -s -L https://nvidia.github.io/nvidia-docker/gpgkey | $ sudo apt-key add -
$ curl -s -L https://nvidia.github.io/nvidia-docker/$distribution/nvidia-docker.list | sudo tee /etc/apt/sources.list.d/nvidia-docker.list

$ sudo apt-get update && sudo apt-get install -y nvidia-container-toolkit
$ sudo systemctl restart docker

nvidia-dockerがインストールされたことを確認

$ sudo docker run --gpus all --rm nvidia/cuda nvidia-smi

Unable to find image 'nvidia/cuda:latest' locally
latest: Pulling from nvidia/cuda
7ddbc47eeb70: Pull complete 
c1bbdc448b72: Pull complete 
8c3b70e39044: Pull complete 
45d437916d57: Pull complete 
d8f1569ddae6: Pull complete 
85386706b020: Pull complete 
ee9b457b77d0: Pull complete 
be4f3343ecd3: Pull complete 
30b4effda4fd: Pull complete 
Digest: sha256:31e2a1ca7b0e1f678fb1dd0c985b4223273f7c0f3dbde60053b371e2a1aee2cd
Status: Downloaded newer image for nvidia/cuda:latest
Thu May 14 16:32:18 2020       
+-----------------------------------------------------------------------------+
| NVIDIA-SMI 440.64.00    Driver Version: 440.64.00    CUDA Version: 10.2     |
|-------------------------------+----------------------+----------------------+
| GPU  Name        Persistence-M| Bus-Id        Disp.A | Volatile Uncorr. ECC |
| Fan  Temp  Perf  Pwr:Usage/Cap|         Memory-Usage | GPU-Util  Compute M. |
|===============================+======================+======================|
|   0  GeForce GTX 108...  On   | 00000000:18:00.0 Off |                  N/A |
| 29%   31C    P8     8W / 250W |      1MiB / 11178MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+
|   1  GeForce GTX 108...  On   | 00000000:3B:00.0 Off |                  N/A |
| 29%   31C    P8     9W / 250W |      1MiB / 11178MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+
|   2  GeForce GTX 108...  On   | 00000000:86:00.0 Off |                  N/A |
| 20%   32C    P8     8W / 250W |      1MiB / 11178MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+
|   3  GeForce GTX 108...  On   | 00000000:AF:00.0 Off |                  N/A |
| 29%   32C    P8     8W / 250W |      1MiB / 11178MiB |      0%      Default |
+-------------------------------+----------------------+----------------------+

+-----------------------------------------------------------------------------+
| Processes:                                                       GPU Memory |
|  GPU       PID   Type   Process name                             Usage      |
|=============================================================================|
|  No running processes found                                                 |
+-----------------------------------------------------------------------------+

現状だとdockerコマンドの前に管理者権限のコマンドsudoが必要

$ sudo docker run ...

これをsudoなしでDockerコマンドを使えるようにする

$ sudo usermod -aG docker $USER
$ newgrp docker

ここまでがDockerの導入．お疲れ様でした....

ようやく次でDockerを導入．

dockerイメージのpull

www.tensorflow.org

gpuサポートかつ，Jupyterを含むイメージをpull*2

tensorflow / tensorflow: のように，カンマの後ろで様々なバージョンのイメージをpullすることができる．

$ docker pull tensorflow/tensorflow:latest-gpu-jupyter

ターミナルでgpuできちんと動くか確認

# 1行目がdockerのシェル内に入って実行，を表す
$ docker run --gpus all -it --rm tensorflow/tensorflow:latest-gpu-jupyter \
python -c "import tensorflow as tf; print(tf.reduce_sum(tf.random.normal([1000, 1000])))"

コンテナ内に入り，ターミナルを起動し，Jupyter Notebookを起動

$ docker run --gpus all -it tensorflow/tensorflow:latest-gpu-jupyter bash

$ jupyter notebook

Jupyter Notebook内でのチェック方法

from tensorflow.python.client import device_lib
device_lib.list_local_devices()

CPUしか認識されてなかったらこれしか表示されない....

[
name: "/device:CPU:0"
device_type: "CPU"
memory_limit: 2789133
locality {
}
]

注意事項 -> gpuを認識させるには docker runコマンドに --gpuオプションが必要．

以下のような定番のコマンドではない

$ docker run -it --rm tensorflow/tensorflow:latest-gpu-jupyter bash

19.03 より前のバージョンでは nvidia-docker2 と --runtime=nvidia フラグが必要です。19.03 以降のバージョンでは、nvidia-container-toolkit パッケージと --gpus all フラグが必要です。

お疲れ様でした自分．

*1:何言ってるのかよくわからない

*2:pullはDockerで使われる用語で，インストールと同じ意味と捉えてOK

2020-04-30

リーダーか，マネージャーか

Books Career 雑記

「リーダー？別に自分とは縁のないこと」のように感じる人は多いと思う．

私もそう．

急にこの言葉を意識することになったのは，とある先輩がくれた本がきっかけである．

2月中，世界はコロナコロナゆうてるけど現在の最先端の医療技術を持ってすれば１ヶ月で鎮火するだろうと軽く考えていたCORONA VIRUS．

お前は強かった．

3月になってもウイルスはおしとやかになる様子は見せず，結局卒業式に予定していた追いコンなどは直前でキャンセルしなくてはならずバタバタだった．

結局研究室でしっぽり送迎会を行うことになったのだが，あまり卒業する先輩とゆっくり話せる感じでもなかったので．

その日，研究室でお世話になった先輩にお礼がてら改めて卒業おめでとうございますの旨を伝えた．そしたら

「なんかいい感じの本置いといたから読んでみて」

その人は分析力・インフラ知識を研究室内の他の誰よりも持っていて，研究プロジェクトをリードし，論文も提出，

日頃から研究室全体のセキュリティ関連を支えるだけでなくて，後輩育成や周りへの配慮を怠らない．しかも全く驕り高ぶらない．

たまに「仏ですか？」と思うほどの徳がある人で

私にとって一番身近ないわゆる「リーダー」だった．

なんの本じゃろ〜〜技術書かな〜とか思いながら翌日みてみるとこれだった

リーダーシップの旅見えないものを見る (光文社新書)

作者:野田智義,金井壽宏
発売日: 2007/02/16
メディア: 新書

ええええええ

うちの研究室には「室長」なる存在がいる．

本をくれた人は室長だった．

室長と言うと仰々しい雰囲気なのだが，研究室全体のイベントとか連絡事項まとめたりする感じで，決して権力を振りかざすポジションではない．

このポジションはボスが勝手に任命するもので，ある日気づいたら自分が任命されていた．

そんな感じで自ら立候補する訳でもなく完全に「与えられる」ポジションだったから

この本をもらったのは少しびっくりしてしまった．

しかし如何せんその本の内容にハッとさせられることも多かったので，備忘録がてらまとめる次第である．

リーダーシップとは

リーダーシップは，特別な人だけがなれるものではなく，全員に開かれたその人のの生き方であり，プロセスを経て結果として「なっているもの」である．

本書では，リーダシップをプロセスとして捉え，それを「旅」になぞらえている．

つまりリーダーシップとは，

リード・ザ・セルフ：自らをリードする
リード・ザ・ピープル：人々をリードする
リード・ザ・ソサエティ：社会をリードする

の3段階を段階を踏んでいくことで形成されるものであり，

特に「リード・ザ・セルフ」を促進させる「リーダーシップのエッセンス」として

「見えないものを見て，それを実現させたいという思い」

を強調している．

例えば，今の自粛期間のある日のことを考えてみる．

仲のいい大学生5人がZoomで集まり，この自粛期間に何か面白いことをしたいという話になった．

その中のA君が「Zoomで，オンラインボードゲーム(例えばカタン)をやらないか」と提案し(実際にカタンがオンラインでできるかは置いといて)，

実際にオンラインでのやり方を教えてゲームが始まった．

他の4人が言い出しっぺのA君の提案に付いていってやってみた結果，ワクワクするようなひと時を過ごせることができたとしたら，

A君は，ささやかながらリーダーシップを発揮したことになる．

A君は最初はリーダーでもなんでもなく，「みんなと自粛期間を楽しく過ごしたい」という思いだけがあった．

その思いを胸に行動(提案)した結果，周りの友人がついて来てくれ，望んだことを実現することができた．

やりたいことを達成し，後から振り返ってみると，A君はリーダーだったのである．

ポイントは，リーダーは権力や権限，地位を利用してではなく，

「その人自身」の存在や感情，行動により人を動かすということだ．

この観点からみると，「リーダー」と「マネージャー」は似て非なるものである．

リーダーとマネージャーの違いとは

リーダーシップを，「フォロワーを束ね，ベクトルを合わせて，求められる方向に導く」ことと勘違いする人は多い．

これは少しずれていて，「マネジメント」と混同している．

本書では，リーダーシップとマネジメントの違いが3つ述べられている．

「見える」か「見えないか」
リーダーは「見えないもの」を見ようとして新しい世界を創ろうとする．
一方マネージャーは，「見えるもの」を分析し，問題を解決することで組織の安定化に寄与しようとする．
「人としての働きかけ」か「地位としての働きかけ」か
リーダーは，人々の価値観や感情に訴え，共感や賛同を経て周囲を巻き込んでいくのに対し，
マネージャーは，すでに与えられている権限や地位を利用してチームの構成員に働きかける．
「シンクロ(同期化)する」か「モチベートする(動機付ける)」か
リーダーは，ビジョンに共感してくれるフォロワーの自発的な行動を誘発するのに対し，
マネージャーは人々の行動を管理し，同じ方向に進ませようとする．

リーダーシップの旅を阻むもの

自分が本当に望んでいること，人生で実現したいこと，貢献したいことに向けて旅の一歩を踏み出すことはそう簡単ではない．

まずは，なぜ今の仕事をしているのか，その会社や組織で働くことにどういう意味があるのかを一度立ち止まって熟考する必要がある．

キャリアとは，「たった一回限りの自分の人生を運ぶもの」という意味で，馬車や車と道後lげんであり，馬車が去って行った後の轍(わだち)がキャリアに他ならない．その足取りを見てこそ，これからどう歩むべきかが垣間見れる

夢なんか実現しっこないという人もいるが，実は夢しか実現しない (TSUTAYAを展開するカルチュア・コンビニエンス・クラブ社長，増田宗昭)

しかし多忙な現代人は，目の前の仕事をこなす忙しさを理由に，本当に自分のやりたいことや解決すべき課題から目を逸らしたまま(=アクティブ・ノンアクション)の人が多い．

アクティブ・ノンアクション... 毎日を多忙に過ごしているにも関わらず，本当に必要で意義があり，真の充足感をもたらす事柄には全く手をつけられていない状態．

これ以外にも本著では様々な名言が登場してきていて，

ひたすら自分の心に響いた．

「アクティブ・ノンアクション」

これなんかは，学生も思い当たる人も多いのではないだろうか．

自分も例外ではない．やりたいことは実現させてきたと思いつつ，1日1日を振り返ると研究室の色々な仕事を言い訳に忙しい「風」になってたことも多い．

早いうちから自分がやりたいことを見出し，自分のスキルで生計を立ててる人，実現したいサービスを起業する人，そんな人はわずかである．

でも，「自分がどんな人間でありたいか」「何がしたいのか」

これは常に追い求め続ける姿勢を持ち，一度見出したらその気持ちに忠実に従い，覚悟を持って人生の進む道を変えられる人間でありたい．

最後に

タイトルにもある「リーダー」か「マネージャー」か．

これはどっちが悪くてどっちがいいと言ってるわけでもないし，
自分はどっちを目指そうという答えを持っているわけでもない．

正直リーダーだのマネージャーだの肩書きはどうでもいいなと思ってる．

少なくとも「この人と一緒にいて，仕事ができてよかったな」と思われる人間であればいいような気がする．

2020-03-28

1年に2回くらい

雑記

一気にドバーッと目から水が出る日がある．今日はそのうちの1日だった．

こんな話をなんで書くのかというと，

今日1日そのものがなんだか色々なことがあったというのと，

最近の異常な日常ということと，

久しぶりに一気に泣いて，「ああこれまた出会ったわ」と，旧友に再開したかのような懐かしい感覚と．

色々記録に残したくなったからである．

涙が大量に流れた原因は，単純で

「自分の無能さに打ちのめされたから」

である．

ここのところずっと，論文の追試実装がうまくいかず頭を悩ませていた．

アルゴリズムは，論文を書いた先生がいる研究室のポスドク外国研究生Aさんともコンタクトを取りつつ，合っていそうだということを確認していた．

しかしそこから先のデータの予測精度が全くでなかった．

過程のデータの可視化を行っておかしそうなところの目星はなんとなく考えつつ，肝心の原因はどうしてもわからなかった．

「同じ問題に毎日頭を悩ませるのも馬鹿らしい．

他の実験を進めるうちに原因が明らかになるかもしれない」

そう思いながら，時間がすぎていた．

今月からそのコンピュータサイエンス専攻(CS)の先生とも2週間に1回合同ゼミを開催することになり，

毎回のゼミで進捗を生まなければならないという圧力を感じていた．

前回のゼミでここがうまくいっていませんというのはすでに報告しており，今回のゼミでは原因を解明して望もうと思っていたのに．

結果を出すことは諦めて，詳細な実験過程を乗せることで乗り切ることにした．

Aさんも，うまくいっていないといっていたし．

そのゼミがどうだったかというと，

それはもう最悪なものだった．

ゼミでは，まず私の方から現状を共有した．

irisレベルの簡単なデータを用いていても精度のベンチマークを達成していなかったことに対し，CS専攻の先生方は難色を示した．

先生はmatlabを使っていたこともあり，その場で私が書いたpythonコードを1行1行確認するわけにもいかない．

「研究を進めるにも，まず簡単なデータでさえ結果が出ないのは問題」

とりあえずそのまま進めて他の手法も試していけばいいのではないか．と考えていた私に，重く突き刺さった．

その場で思わずAさんに現状を聞いてみると，

どうやらAさんは，コンディションによってはうまくいかないこともあるが，概ね論文の結果は少なくとも簡単なデータで再現できているとのことだった．

ああ，再現できてたのか．

私，1ヶ月くらいかけてたのに，うまくいかない原因もわからず，

全然進んでいない．

CS専攻の先生とAさんはそのまま，Aさんから聞いた現状を踏まえ，より応用的な手法について議論を始めた．

置いてかれてるなー．研究室のメンバーに申し訳ない．

その2人の様子を見ながら，ぼんやりと思った．

見かねたこちらのボスが間に割って入って，Aさんに．コードを共有するよう，いつものハツラツとした強い主張の声でお願いした．

我々は，Aさんからコードを共有して，まず学ぼう，と．

すごいなぁ．よくこの空気感の中，割って入ってお願いできるなぁ．

申し訳ない．

ボスの図太さに感嘆すると同時に，

私は，そんなことを言わせてしまったボスに対して，また，居心地悪い思いをしているであろう同じ研究室の同期後輩に対して情けない気持ちでいっぱいになった．

冷静に考えて，「わかりません，うまくいきませんでした」を報告することにはなんの価値もない．

どれだけ頑張っても，評価されるのはその根性ではなく，アウトプットだ．

研究だけでなく授業や打ち合わせ，会議や雑務も抱えている先生方からしてみれば．

「わからなければ個人で解決しとけよ」という話である．

私はそれをやろうとしなかった．

単純に，

悔しかったから

である．

Aさんからしてみれば自分の研究テーマでもあるわけだし，

「コード見せてください」

と軽々しくお願いすることは私がまるでAさんがこれまで大切に時間をかけて作ったケーキを横取りするような感覚だった．

振り返ってみれば，単なるプライドでしかない．

分からなければ，分からないと主張しないと，何も生み出せないし，

その結果有意義な時間を過ごせず迷惑がかかるのはAさんをはじめとするゼミ参加者10人以上全員なのである．

「考える」ことと「悩む」ことは違う．

「考える」とは，「答えがある」という前提の下，建設的に要因を検討すること
「悩む」とは，「答えがない」という前提の下，「考えるフリ」をすること．

イシューからはじめよ――知的生産の「シンプルな本質」

作者:安宅和人
発売日: 2010/11/24
メディア: 単行本（ソフトカバー）

私は，「考えるフリ」をしていたらしい．

自分では答えが探せないとわかっていた．

なのに，だらだら，

「なんでなんだろう」「どうしてうまくいかないんだろう」と

自問自答して時間を溶かしていた.

ゼミが終わり，

CSの先生から自分宛に励ましとも取れるメールを見て，

情けなさに目の前がかすみそうになるのを堪え

メールの返信を打つ．

「指導ありがとうございます。頑張ります、今後ともよろしくお願いします」

的な文面

すぐに1分後にボスから返信

「さすが，ありがとう」

さすが？？？何が？どこが？？？？？

この文面を見た瞬間，糸が切れた完全に．

意味わからん．

私が全然できないのわかってるだろ．

自分の一体全体どこを評価してくれているのか，さっぱり理解できなかった．

なんだか信じられているらしいことだけはわかった(この前にメッセンジャーも来ていた)

ある心理学の実験によると，指導者が教え子の可能性を本気で信じ，本人に才能があると思わせることは，そうされなかった人と比べて有意に成績や結果を出すことができるそうだ

優れたリーダーは，本気で人の可能性を信じることができる．

信じられていると自覚した人は，それに応えようと一生懸命努力する．

それが違いを生むらしい．

GIVE & TAKE 「与える人」こそ成功する時代 (単行本)

作者:アダムグラント
発売日: 2014/01/10
メディア: ハードカバー

まだ自分のことで精一杯な私は，人を信じることができる器になれるだろうか．

または人に逆に期待されたとして，それに応えることができるだろうか．

確実に言えるのは，「自分にだけには負けたくない．」ということだ

涙腺が崩壊したその1分後には，家をでなければならない時間が15分後に迫っていることに気づき，大慌てで化粧直しをして支度をし，家を飛び出した．

どこか他人事だと思っていたCOVID-19がいよいよ大規模流行の局面となり，3/27には外出自粛要請が出された．

そんな最中，私は東京へ行く準備をしている．

気づかない間に満開となった桜と，

気づかない間に蔓延していたCOVID-19.

見えないウイルスに対し活動が忍ばれている中，居酒屋に集う人．

健康面でも財政面でも影響を受ける人が多い中，目の前のアルゴリズムだけを考える自分．

全てが異様でちぐはぐな世界にいる．

なんとか滑り込んだつくばエクスプレスに乗りながら思った．

結局，どんなに恥ずかしくても，惨めでも，生きていくしかないんだけどね

f:id:wimper_1996:20200328015013j:plain — 鬼滅の刃より

f:id:wimper_1996:20200328015008j:plain — 鬼滅の刃より

2020-02-25

50行くらいで実装するニューラルネットワーク

Deep Learning 機械学習

これ何
ニューラルネットワークは何をしているのか？
- 順伝播(forward propagation)とは
- 逆伝播(back propagation)とは
実装
最後に

これ何

classもdef文も書かずに, 隠れ層1つのニューラルネットワークを一から実装します.
実装するに当たって、順伝播と逆伝播の考え方は
Coureseraのdeep learning specializationが大変役立ちました*1。

サイトとしてはhttp://cs231n.github.io/neural-networks-case-study/を参考にしました。ただ、逆伝播について、より数学的に厳密に実装したつもりです。

実装したニューラルネットワークは下図のようになります。
f:id:wimper_1996:20200225021239p:plain

上付きの[]数字は何番目の層か、ユニットの個数は特徴量の数とみなせます。
斜め文字W, bは行列です。

特徴は

出力層ユニット1の２値分類を扱う
最も単純な2層からなるニューラルネットワークを扱う
活性化関数はシグモイド関数
入力層ユニット数は2(つまり特徴量２), 隠れ層ユニット数は4

なお、ニューラルネットワークにおける層の数は, (隠れ層の数) + (出力層の数) としてカウントされ、入力層は含まれません。

2層以上で構成されるモデルは多層パーセプトロン(Multi Layer Perseptron: MLP)と呼ばれ、

深層学習(deep learning)とは、一般的に3層以上で構成されるMLPモデルを用いた機械学習のことを指します。

ニューラルネットワークは何をしているのか？

実は、そこまで難しくありません。
ニューラルネットワークは、ロジスティック回帰です。

流石に嘘です。でも、とても近いです。
ロジスティック回帰式は、線形回帰式を非線形活性化関数であるシグモイド関数の中に入れてあげることで、0以上1未満の２値分類を表すことができるのでした。
それと同じで、

ニューラルネットワーク = 線形結合 + 活性化関数による非線形変換

と言えます。
順伝播のセクションをみるともうちょっとイメージ湧くはずです。

さて、ニューラルネットワークの1回(1 epoch)あたりの学習の流れは以下の通りです。

重みを初期化する

順伝播により出力層に重みを伝え、確率を算出する

逆伝播により重みの差(勾配)を計算する

重みを更新する

2番目と3番目、一度は聞いたことがあるであろう「順伝播」と「逆伝播」を説明します

順伝播(forward propagation)とは

入力層から出力層に向けた伝播を表します。こちらはイメージしやすく、線型変換 + 非線形変換を経て、最後に確率を計算する流れです。
単層パーセプトロンで見てみます。
これは、ロジスティック回帰と全く同じ計算となっています。
図1. 単層パーセプトロン(ロジスティック回帰)
2値分類では、出力層をsigmoid関数とすることで、0以上1未満の値を出力することができます(つまり活性化関数の出力aがそのまま予測値 $\hat{y}$ になる)。 $\hat {y} = 0.8$ の場合、ラベル1となる確率が0.8ということです。
そして、予測値aと、真値yからコスト関数L(a, y)が求めます。

同じことが3層以上のニューラルネットワークでも言えます。

逆伝播(back propagation)とは

逆伝播はイメージつきにくいかもしれません。
ポイントは

重みを更新するために、誤差に基づく重みの差分(勾配： $dwやdb$ )を求めたい

ということです。差分がわかれば、
$\displaystyle W = W - \lambda dw$
のようにして、初期値Wから重みを更新をすることができます。ここでの $\lambda$ は学習率というやつです。
じゃあ、どうやって求めるのか。
「合成関数の連鎖積」を使います。
ここは数学的知識がある前提で進めます...
図で見るとこんな感じになります。
図2. 単層パーセプトロンでの逆伝播
この例では、 $dw_1$ を求めたいとします。
右から見てみてください。

コスト関数L(a, y)がわかっているので、Lのaに対する偏微分daが求まる

次に偏微分dZを求めたいが、 $\displaystyle \frac{ \partial L }{ \partial Z }$ を直接求めるのではなく、合成関数の連鎖積で $\displaystyle \frac{ \partial L }{ \partial a } \frac{ \partial a}{ \partial Z }$ (青とピンクに)まで分解し、既に既知のdaと $\displaystyle \frac{ \partial a}{ \partial Z }$ を用いて計算する。

同様に、dw1も、合成関数の連鎖積で、既知のdZと $\frac{ \partial Z}{ \partial w_1}$ を用いて計算する。

ここで用いている偏微分da および $\displaystyle \frac{ \partial a }{ \partial Z }$ は、
コスト関数として２値分類で用いられる交差エントロピー(1サンプルあたり)
$\displaystyle J = y\log a + (1-y)\log (1-a)$
およびシグモイド関数
$\displaystyle a = \sigma(Z) = \frac{ 1 }{ 1 + exp(-Z) }$
の偏微分を求めています。

dZまで実際に計算してみると、a - yと、こんなにスッキリした値になるんですね。
ぜひ、実際に手を動かして確認してみてください。

「逆伝播」と言っている通り、1→3、順方向とは逆の流れで重みが伝播しているのがわかります。
後はひたすら、

順伝播で確率aを計算

コスト関数を計算

逆伝播により勾配を計算

重みを更新

これをループで繰り返します。

実装

# ライブラリのインポート import numpy as np import matplotlib.pyplot as plt %matplotlib inline import sklearn from sklearn.linear_model import LogisticRegressionCV from sklearn.metrics import accuracy_score # データの生成 from sklearn.datasets import make_moons X, y_ = make_moons(n_samples=100, random_state=0, noise=.3) y = y_.reshape((y_.shape[0], -1)) print(X.shape) # (100, 2) print(y.shape) # (100, 1) # 描写 plt.scatter(X[y_==0, 0], X[y_==0, 1], color='r', marker='^', alpha=0.5) plt.scatter(X[y_==1, 0], X[y_==1, 1],color='b', marker='o', alpha=0.5) plt.show()

データ数100, ラベルは0か1, 特徴量すなわち次元数は2のデータです。
ちなみにsklearnで色々なデータが入っててこの半月状のデータもあることは知ってましたが、引数にnoiseも設定できるんですね。便利。

まずは古典的なロジスティック回帰をみてみます

# Train the logistic regression classifier clf = LogisticRegressionCV() clf.fit(X, y_) # Print accuracy y_pred_lr = clf.predict(X) score = accuracy_score(y_, y_pred_lr) print ('Accuracy of logistic regression: %d ' % (score * 100) + '% ' + "(percentage of correctly labelled datapoints)")

色ぬりもしてみるとこんな感じになりました

必要な関数はシグモイド関数a = σ(Z)でこれは作っておきます

def sigmoid(x): return 1 / (1 + np.exp(-x))
ここからは、

ニューラルネットワークの構造の定義

重みの初期化

ループで重みを更新

です。

# back propagationにおける勾配は全て、合成関数の連鎖積を計算しています。
コスト関数は、mサンプル全体だと次のようになります。

ここでのa[2]は実装におけるy_outと対応しています。
ここで、1サンプルあたりの、実装されている勾配の数式をまとめると次のようになります。
ちょっとわかりにくいですが、全ての値は行列だと思ってください。

$dz_2 = y_{out} - y$ (図2における2. a-yに対応)
$dw_2= a_1^T dz_2$
$db_2 = dz_2$
$dz_1 = (dz_2 w_2 ) * a_1 * (1-a_1)$ (*は単純な(要素同士の)掛け算, da/dz = a_1 * (1-a_1)を利用)
$dw_1 = x^T dz_2$
$db_1 = dz_1$

注意点

図2では単層だったためZやWが一つしかないが、今回は２層なのでdW1やdb1も求める必要がある。ただ、同じ(線型結合+sigmoid)が加わっただけで逆伝播も同じように計算できる。

サンプル全体のコストを求めているので、サンプル数(m, コードではn_samples)で割り一つの重みの変化に対応させる。勾配も。

行列演算上そのまま内積を求めるのではダメで、転置する必要がある

# 1. Define neural network stracture n_x = X.shape[1] # 特徴量の数がinput n_h = 4 # 適当, 今回は4ユニット n_y = 1 # 2クラス分類は1つの確率で決まるので、1ユニット num_iteration = 15000 # 何回計算するか n_samples = X.shape[0] # サンプル数 # 2. Initialize the model's parameters W1 = np.random.randn(n_x, n_h) * 0.01 W2 = np.random.randn(n_h, n_y) * 0.01 b1 = np.zeros((1, n_h)) b2 = np.zeros((1, n_y)) # 3. loop for i in range(num_iteration): # forward propagation Z1 = np.dot(X, W1) + b1 # 線型結合(隠れ層) A1 = sigmoid(Z1) # 活性化関数(隠れ層) Z2 = np.dot(A1, W2) + b2 # 線型結合(出力層) assert Z2.shape == (n_samples, 1) y_out = sigmoid(Z2) # probability(0~1), y_out = a2 # cost function cost = -1 / n_samples * np.sum((np.log(y_out)*y) + (np.log(1-y_out))*(1-y)) assert(isinstance(cost, float)) # back propagation dZ2 = y_out - y dW2 = np.dot(A1.T, dZ2) / n_samples assert dW2.shape == W2.shape db2 = np.sum(dZ2, axis=0, keepdims=True) / n_samples dZ1 = np.dot(dZ2, W2.T) * (A1 - np.power(A1, 2)) dW1 = np.dot(X.T, dZ1) / n_samples db1 = np.sum(dZ1, axis=0, keepdims=True) / n_samples # update parameters lr = 1e-0 W1 -= lr * dW1 W2 -= lr * dW2 b1 -= lr * db1 b2 -= b2 * db2 if i % 1000 == 0: print('iteration %d:loss %f' % (i, cost))
15000回目のイテレーションで出力された結果y_outをみてみる

# 出力された確率が0.5以上だったらラベル=1, それ以下だったらラベル=0 y_pred = np.where(y_out < 0.5, 0, 1) print('training accuracy: %.2f' % (np.mean(y_pred == y)))
training accuracy: 0.97

こんな感じになりました。

最後に

簡単そうに見えますが、全然大変でした。
ひたすらassert文で自分の期待する行列のshapeと一致するか、手探りで進んでいった感じです...
コツとしては、ひたすら「行列の形を意識すること」だと思います。

ユニット数は次元数と同じとみなせるので、データの形は基本(n_samples, ユニット数)なはず

コスト関数はfloatなはず

など、色々なポイントがあるので、逐一チェックするといいと思います。

1から理解しながら実装するのはかなり大変ですが、これをやると例えば

初期値や学習率をどう決めるのがいいのかが(解説読んですんなり)わかるようになる

sigmoid関数以外のtanhやReLUが良いのはなぜかわかるようになる

CNNや最新のディープラーニング技術も(雰囲気)わかるようになる

Inputするデータの形をめちゃくちゃ意識するようになる

行列演算ちょっとできるようになる

などかなりメリットがあるなと思います。

ディープラーニングの闇の魔術に飲み込まれない程度には理解したいところです。
最後まで読んでくださってありがとうございました〜

*1:自分は1ヶ月かけて5つのコースを終えることができました.

wimper_1996 2020-02-25 03:13 読者になる

広告を非表示にする

もっと読む

コメントを書く

2020-02-22

正則化とはいったいなにでどうして過学習を防ぐのか

機械学習

正則化って何をしているんですか？？？？

予測モデルのバリアンスを小さくし未知データに対する汎化性能を高めるのに有効な手法でしょ？

その手法としてL1正則化とかL2正則化とかあるよね

コスト関数に、ペナルティとして正則化項を加えるんだよね

.....。分かっているようで実態が分かっていない。

…そもそもバリアンスが高いってなんだっけ....？？

そもそも正則化項ってなに？

ペナルティとしてモデルのパラメータ(正則化項)を加えたらなぜ過学習が抑えられるの？

「バリアンスが高い」ってなんだっけ？

「過学習を起こしている」と同義。
手元のトレーニングデータで学習をしすぎた場合、未知のテストデータだと予測精度が下がってしまうという過学習が起こる。
逆に、作成した手元のデータで予測精度が悪かった場合、学習不足と呼ばれる。これは元も子もなくて、普通学習データで良い精度を出した上でいかに過学習を抑えるかが重要である。
「過学習」と「学習不足」は直感的に分かりやすいが、これら以外の説明用語もよく出てくるのでまとめてみる

過学習学習不足

バリアンスが高い (High variance) バイアスが高い (high bias)

予測結果のばらつきが大きい予測結果が真値から外れている

汎化性能が悪い (予測精度が悪い)

モデルが複雑モデルが単純

言葉とイメージを対応させて覚えると良いように思う
高バイアス＝予測精度が悪い＝左
高バリアンス＝ばらつきが大きい＝右
イメージ図1

また、的を用いた例もよく見られる。
的の中心が真値だとすると、予測結果(矢の中心)が中心に近いほど精度が高くバイアスが小さい(左列)
そして、矢の中心が試行のたびにあちこちにあたると、汎化性能が悪くバリアンスが高い(下行)
1が最高、4が最悪。
2は、低バリアンスだけど高バイアス。
試合でも動じなくて丁寧なんだけどあんまり最高点取れない....
3は、低バイアスだけど高バリアンス。
練習には強いんだけど試合になるとたまに崩壊するパターン

1行目の「バリアンス(variance)」と「バイアス(bias)」は頻出だが、言い回しが似ているので非常に混乱しやすい。
日本語だと過学習／学習不足の方が分かりやすいので、varianceとbiasに関してはどっちがどっちだっけ？となってしまう。
しかし、英語だとこのvarianceとbiasの表記の方がよく目にする。過学習の英語版overfittingもよく見るけれど、英語ドキュメントを読んでいくに当たっては前者の言い回しに慣れておくのがベター。

なお、バリアンスとバイアスの問題はトレードオフと言われる。
つまり、トレーニングデータで予測精度を向上させようとすると(Low bias)モデルが複雑になりすぎてしまい、未知データに対する汎化性能が小さくなってしまう(Hign variance)。

正則化とは

予測モデルの汎化性を高めるために、最小化させたいコスト関数に「正則化項」を加えること。

i番目のサンプルの予測結果を $\hat{ y } ^ { (i) }$ 、真値を $\ y^{ (i) }$ で表し、一つのサンプルに対する損失関数をLで表す*1。
最終的に最小化させたいコスト関数Jは重みwを用いて以下のように表せる*2。

$\displaystyle y = J (w) = \sum_{ i = 1 }^{ n } L(\hat{ y } ^ { (i) }, y ^ { (i) })$

正則化は式で書くと

$\displaystyle y = J (w) = \sum_{ i = 1 }^{ n } L(\hat{ y } ^ { (i) }, y ^ { (i) }) + \lambda \| w \|^2 - (1)$

のように表せる。ここで、コスト関数に加えた項を正則化項と呼ぶ。

言葉で言い換えると

予測モデルで学習した重みの大きさを、追加のペナルティとしてさらにコスト関数に加えること

であることがわかる。
正則化項は大きく分けて2つある。

L1正則化項： $\ \lambda \| w \|^2$ (上式)

L2正則化項 : $\ \lambda \| w \|$

この二つ。
そして、この項を加えた線形回帰手法として、

L1正則化項を取り入れたLasso回帰

L2正則化項を取り入れたRidge回帰

両者を取り入れたElastic Net

この３種類があげられる

なぜ正則化が過学習を防ぐのか

よくある説明が、二次元データに対する単純な最小誤差問題 $\ \sum_{ i = 1 }^{ 2 } (\hat{ y }^{(i)} - y^{(i)} )^2$ を考え、重みw1とw2を求めるという問題を想定した図である
図2(https://tjo.hatenablog.com/entry/2015/03/03/190000より一部改変)

2次元データで考えた場合、
ペナルティとしての正則化項L2ノルム(E(w) = $\displaystyle\lambda \|w\|^{2}$ )と、
元の単独のコスト関数 $\displaystyle J(w) = \sum_{ i = 1 }^{ 2 } (\hat{ y }^{(i)} - y^{(i)} )^2$ は、どちらも円で表される。
そして、E(w)とJ(w)は半径とみなすことができ、半径の和の最適化問題に帰着するので、直線上で接した状態が最も最適な状態となる。
それが上図。

要はw1,w2からなる重み付けベクトルの空間上に学習データに対する誤差項の広がりを配置しこれを動かすことで誤差を最小化させるわけですが、そこにペナルティ項を付けておくことでw1,w2の定まり方が変わるというお話です。左側のL1ノルム正則化であれば尖った形の領域に接するようにしなければならないため自ずとw2の軸上に最適点が定まってw1=0となり、右側のL2ノルム正則化であれば円状の領域に接するようにしなければならないためw1,w2ともにnon-zeroな値が入る、という感じになるわけです。

RでL1 / L2正則化を実践する - 渋谷駅前で働くデータサイエンティストのブログ

....わかるようで、わからない。
本当は、コスト関数J(w)をゼロに近づけたい。つまり、右上の楕円のオレンジの中心に行きたい。
しかしながら、ペナルティ項E(w)も入れてしまっており、w1とw2は青い網かけの円を出ることはできない。
(定義 $\displaystyle\lambda \|w\|^{2} = w_1^2 + w_2^2$ から、w1とw2は円の外の値はとりえない)
したがって、E(w)とJ(w)の和の最適解は、必然的に上図のようにペナルティ項の円とコスト関数の楕円が接した所になる。

さらにもう少し違う観点からイメージが掴めるように説明してみる。
正則化項を付けない状態で学習を進め、モデルのバリアンスが高くなった状態を考える。
バリアンスが高いとは、トレーニングデータを捉えようとするあまりモデルが複雑になりすぎてしまい、過学習を引き起こしているということだった。
複雑な予測モデルとは？？イメージ図１の3つ目の青線のようなモデルのことだ。
再掲
式で書くと、左はシンプルな1次の線形回帰式 $\displaystyle y = w_1x_1 + w_2x_2$ であり、右は3次以上の非線形回帰式 $\displaystyle y = w_1x^{4}_1 + w_2x^{3}_2 + ...$ と表せる。(4次式なのは適当)
モデルが複雑になるほど、次数が増加し、重みwの取りうる値が多様になる。

この状態のコスト関数Jに正則化項が加わるとどうなるか？

そもそも予測モデルは、トレーニングデータ全体の予測値と真値との差、つまりコスト関数が最小になるように学習したいんだった。
(1)式では、元々のコスト関数J(w)に、さらに正則化項が足されている。

つまり、「正則化項も含めた式全体の値を最小にしなければならない」という視点で考えてみると、
wが多様な値をとれば取るほど、正則化項の値が大きくなり、コスト関数J(w)も大きくなることがわかる。
そしてハイパーパラメータ $\lambda$ の値が大きくなればなるほど、正則化項 $\lambda \|w\|^2$ の大きくなるスピードも早まり、重み係数の大きさが小さくなるよう圧迫される。
つまり、トレーニングデータのyを捉えるために出てきた $\displaystyle x^{4}$ のような大きい次数の重みほど、ゼロに近づき、シンプルな式に近づく。
しかし $\lambda$ を大きくし続けシンプルな式に近づきすぎると、重み係数が全て小さくなってしまい、今度はバイアスが大きくなってしまうので、バイアスとバリアンスのバランス(紛らわしい)が取れたかな？と思うパラメータの調整が必要だ。
実際にモデルに正則化項を取り入れる場合、sklearn.linear_modelから直接適切なモデルを選択すれば良い。
ネットに山ほど情報が載っていると思うのでpythonを用いた例はそちらに...
(1ヶ月ぶりに書いて力尽きました)

機械学習の分野は膨大で、いちいち数学的な証明までできるようになっていては首が回りませんが、盲目的にscikit-learnやKerasといったツールを用いるだけでなくて常に言葉で理由を説明できるようにはなりたいと思うこの頃。
最後まで読んでくださってありがとうございました〜！！

*1:Coursera deep learning AI コース( Neural Networks and Deep Learning | Coursera )によると、一つのサンプルにおける、最小化させたい目的関数を「損失関数」といい、サンプルデータ全体に対しては「コスト関数」と言うらしい

*2:バイアス項bは省略する

wimper_1996 2020-02-22 22:05 読者になる

広告を非表示にする

もっと読む

コメントを書く

2020-01-23

最低限仲良くなりたい頻出な数式や統計量の行列表現

線形代数確率統計

これ何

これまでなんとなく曖昧で避けてきてもなんとかなってきたけど、機械学習を勉強するに当たって当たり前のように出てくる数式や統計量の行列表現を当たり前の知識にする！
僭越ながら、機械学習を勉強すると、様々な理論が固有値問題や単純な確率統計が土台となることを痛感します。
逆にいうと、ベースを固めてしまえば、新しく学ぶ機械学習の理論もスムーズにインプットできると感じます。

まずは、数式の内容自体は簡単だけど見た目が記号になると慣れ親しんでないが故に一気に難しく感じる、ベクトルや行列表現の食わず嫌いを克服したい。
食べ物でいうとなんとなく崇高で見た目もまずそうだけど美味な「うに」を徐々に克服しようといったところ*1。

どんな人向け

例えば、3つの特徴量からなるデータがあった時、１つのサンプルデータ $\vec{x} = (x_1, x_2, x_3)$ を特徴量 $\vec{w} = (w_1, w_2, w_3)$ で重みづけして予測値yを表現するとするなら、
$y = w_1x_1 + w_2x_2 + w_3x_3$
と明示的に表現されればすんなり理解できるけど
より一般化して
$y = \boldsymbol{ w }^{\mathrm{T}} \boldsymbol{ x }$
と書かれるのは最初は「😇」となっちゃいがちな人*2。
はい、私もです。

一般的なデータのまとめ方

これまで機械学習を学んできて、基本的には

1行が1サンプル

1列が1特徴量

が原則*3。そして、

特徴量=次元の数

である。
i番目のトレーニングサンプルのj個目の特徴量のデータは $x_{ij}$ と表現される。

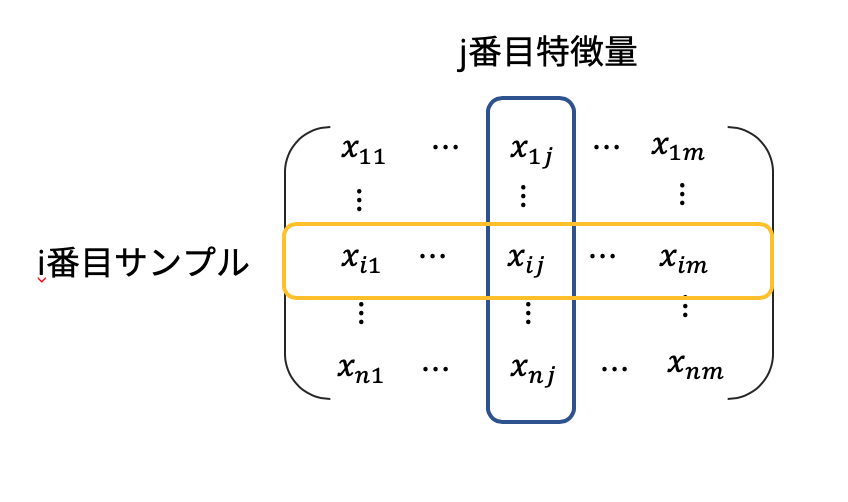
太字のアルファベット $x$ は通常[列ベクトル]を表すと言っていい。
つまりj個目の特徴量を表す列ベクトル $x_j$ (j次元, j変量とも言う)は
$\boldsymbol{ x }_j = \left( \begin{array}{c} x_{1j} \\ x_{2j} \\ \vdots \\ x_{nj} \end{array}\right) = (x_{1j}, x_{2j}, \ldots, x_{nj})^{\mathrm{ T }}$

となる。ここまでは、基本の基本。

行列計算で意識してほしいこと

機械学習においてnumpyを使った行列計算は頻出。

import numpy as np a = np.dot(b, c)
これは、行列積 $A = BC$ を表す。
このような行列計算を行う際、必ず意識してほしいこと。

行列の行と列の数をチェックする

行列積の計算では、必ず、各要素の外側の行と列が残る。どういうことかというと

例えば
$\displaystyle \begin{pmatrix} 1 & 2 & 3 \\ 3 & 4 & 5\end{pmatrix} \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array}\right)$
という(2×3)と(3×1)の行列積を考えてみると、答えは $\left( \begin{array}{c} 6 \\ 12 \end{array}\right)$ となり、(2×1)となることがわかる。行列積では、内側の数(今回の場合3)は必ず等しい。
そして、残るのは、１つ目の行列の「行」と、最後の行列の「列」だけである。
色々な行列同士の掛け算を見たとき、まず行と列の掛け算をチェックしてみてください。
それを意識するだけで正しい行列演算にたどり着くことも多く、理解の幅が広がります。
それでは、具体的な式をいくつか見ていきます。

線型結合

冒頭でも触れた例。
m個の重みベクトル $\boldsymbol{ w }$ とデータの入力ベクトル $\boldsymbol{ x }$ を用いて表される予測値 $y$ は、式で書くと

$\displaystyle y = w_1x_1 + w_2x_2 + ... + w_mx_m$

これを行列で表すと、wとxが両方とも縦ベクトルの場合、

$\displaystyle y = \boldsymbol{ w }^{ \mathrm{ T } } \boldsymbol{x}$

となる。w(またはx)どちらかを転置することがすぐわかるようにしましょう。
pythonで書くと

np.dot(w.T, x)
wとxが両方縦ベクトルの場合, そのままだと(m, 1)と(m,1)の行列演算はできないので片方を転置します。
もし自分で行列の形を設定するとき、wを横ベクトルと考えた場合は $\displaystyle y = \boldsymbol{ w } \boldsymbol{x}$ という式になり、

np.dot(w, x)
でOK.
また、これはベクトル $\vec{x}$ からベクトル $\vec{w}$ への射影、すなわち内積を表しているともいえる。

$\displaystyle y = \boldsymbol{ w }^{ \mathrm{ T } } \boldsymbol{x} = w_1x_1 + w_2x_2 + ... + w_mx_m = (\boldsymbol{ w }, \boldsymbol{ x })$

分散(variance)と共分散(covariance)

j個目の特徴量の偏差平方和は、j特徴量における平均 $\mu$ を用いて $\displaystyle \sum_{ i = 1 }^{ n } (x_{ij} - \mu_{j})^2$ と表される。
j個目の特徴量の(不偏)分散 $\displaystyle x_j$ は、偏差平方和を(データ数-1)で割った値である。

$\displaystyle v = s_{jj} = \frac{1}{n-1} \sum_{ i = 1 }^{ n } (x_{ij} - \mu_{j})^2$

共分散は、ある1つのサンプルにおける、2つの特徴量jとkの分散にあたり、 $x_j$ と $x_k$ の偏差積和をn-1で割ったもの。式で書くと

$\displaystyle s_{jk} = \frac{1}{n-1} \sum_{ i = 1 }^{ n } (x_{ij} - \mu_{j})(x_{ik} - \mu_{k})$

これを行列で書く(一般化する)と

$\displaystyle \frac{( X^{ \mathrm{T} } - \mu)(X - \mu)}{n-1}$

となる。各データを正規化(平均をゼロ)して、

$\displaystyle S = \frac{X^ \mathrm{T} X}{ n-1 }$

と書かれることが多い。pythonで書くと

# X.shape = (n_samples, m) であるとする # 正規化して, 共分散行列を求める u = np.mean(X, axis=0) n_samples = X.shape[0] S = np.dot((X - u).T, (X - u)) / (X_train.shape[0]) # あるいはこれで一発 np.cov(X)

この行列の形は何x何でしょうか？

答えは、(mxm)で、特徴量x特徴量の対角行列です(下図)。
対角成分が分散、右上(左下)が共分散となります。
全生徒の、身長, 体重, 靴のサイズ....といった変数の関係性が見たいと考えるとわかりやすいでしょうか。

相関係数

例えばXとYの共分散は、「(Xの偏差) ×(Yの偏差)」の平均であり、２変数間のばらつきを表す指標と言える。
ただ、これだとスケールに依存するという問題がある。例えばXが数学でYが国語の点数である場合、満点が10点か100点かによって値がかなり変わってくる。
共分散をスケール化したものが、相関係数であり、式で表すと

$\displaystyle r_{jk} = \frac{ s_{ jk } }{\sqrt{ s_{ ii } } \sqrt{ s_{ jj } } }$

つまり、共分散を、分散の平方根(=標準偏差)で割ったものである。これを行列で表すと

$\displaystyle R = \frac{X^ \mathrm{T} X}{ \sigma_{i} \sigma_{j} }$

ここで、 $\sigma_{i}$ は標準偏差を表す(= $\sqrt{s_{ii}}$ )。
pythonで書くと

np.corrcoef(X)

固有値問題

これも基礎知識としておくべき事項。
普通、とあるベクトル $\vec{v}$ に行列 $A$ をかけると、回転して向きが変わる。例えば
$\displaystyle \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} \left( \begin{array}{c} 1 \\ 1 \end{array}\right) = \left( \begin{array}{c} 3 \\ 7 \end{array}\right)$
となるが、これは $\vec{v} = \left( \begin{array}{c} 1 \\ 1 \end{array}\right)$ というベクトルが、 $\vec{v}' = \left( \begin{array}{c} 3 \\ 7 \end{array}\right)$ というベクトルに回転＆拡大したと見なせる。
しかし、稀に、行列をかけても回転せず大きさだけが変わるベクトルが存在する。このベクトルが固有ベクトル(eigen vector)であり、変化した大きさを表すのが、固有値(eigen value)である。式で書くと

$\displaystyle A\vec{v} = \lambda\vec{v}$

求め方も一応備忘録として。まず上記の式の右辺を左辺に移行すると

$\displaystyle (A-\lambda E) \vec{v} = \vec{0}$

Eは単位行列。もし $A-\lambda E$ 部分が正則(non-singular matrix / regular matrix)であるとするなら(逆行列を持つなら)、 $\vec{v}$ が0でなければならない。
逆に言うと、 $\vec{v}$ が解をもつ条件は、正則でなくなる条件式、

$\displaystyle \begin{vmatrix} A-\lambda E \end{vmatrix}=0$

を満たせば良い。これが固有方程式と呼ばれるもので、これを解く問題を固有値問題という。
具体的な解き方は教科書などを参照してほしい。
ただ、機械学習において固有値問題を解くときは、numpyのパッケージを用いて

np.linalg.eig(A)
で一発で求まるので、解き方に固執する必要はない。
さて、固有ベクトルを横に並べた行ベクトル $V = ( \vec{v_1}, \vec{v_2} \ldots)$ と、それに対応するように固有値を対角上に並べた対角行列 $\varLambda = \begin{eqnarray}\left( \begin{array}{ccc} \lambda_1 & 0 & \ldots \\ 0 & \lambda_2 & \dots \\ \vdots & 0 & \ldots \end{array}\right)\end{eqnarray}$ を用いて、行列表現を書くとこうなる

$\displaystyle AV = V\varLambda$

ベクトルで書いた式と見比べて、 $V$ と $\varLambda$ の順番が違うことに注意。
Aの右から逆行列 $V^{-1}$ をかけて $A = V\varLambda V^{-1}$ となる。
この時、固有ベクトル同士は独立であり、正規直交基底をなす。つまりVは直交行列である。よって $V^{-1} = V^{\mathrm{T} }$ であることを用いて

$\displaystyle A = V\varLambda V^{\mathrm{T}}$

これを、「Aの固有値分解」あるいは「対角化」という。
必ず、正方行列(n×n)＝正則行列(n×n)・対角行列(n×n)・正則行列(n×n)の形になる。

何が嬉しいの

2つある。
1つ目。嬉しいというか、必要です。
機械学習の理論でバンバン出てきます。
主成分分析(Principal Component AnalysisPCA)や、特異値分解(Singular Value Decomposition: SVD: )、線形判別分析(Linear Discriminant Analysis: LDA)といった「次元圧縮」は、この固有値分解がベースといってもいい。
固有値分解の形は必ず理解しよう。
2つ目。少し蛇足かもしれないが、もともと対角化は、 $A^{n}$ を求めるために編み出されたもの*4らしい。
なぜかというと
$\displaystyle A^{n} = (V\varLambda V^{-1})^{n} = (V\varLambda V^{-1})(V\varLambda V^{-1}).... = V\varLambda^{n} V^{-1}$ が成り立つから。( $VV^{-1} = 1$ で全て打ち消される)

$\varLambda = \begin{eqnarray}\left( \begin{array}{ccc} \lambda_1^{n} & 0 & \ldots \\ 0 & \lambda_2^{n} & \dots \\ \vdots & 0 & \ldots \end{array}\right)\end{eqnarray}$

を見ると、対角成分以外は全てゼロだし、行列Aをn回掛け算するよりもいかにも簡単に求まって嬉しそう。
対角化もろもろについてはこのブログが詳しいのでぜひ。
kriver-1.hatenablog.com

その他呼吸するがごとく当たり前にしたい数式や記号など

$\| w \| = \sqrt{w_1^{2} + w_2^{2} + ... }$

ノルム：ベクトルの重みの二乗和の平方根(つまり大きさ)
これを行列で表すと

(発展) $\| A \|_F = \sqrt{ \sum_{ i,j }^{ m,n } a_{ij} }$

Frobeniusノルムといい、全成分の二乗和の平方根である。Fの添字がつくことが多い。

pythonでは

np.norm(x)
(ここまで見たように、数値演算では関数が実装されていることが多いnumpyを活用しまくります。)

$\boldsymbol X \in \mathbb{ R }^{n×m}$

n×m次元 = n個のデータとm個の特徴量からなる実数空間に属するX。

合成関数の微分 $\frac{ \partial f(z) }{ \partial z }$ の求め方

シグモイド関数 $a = \sigma(z) = \frac{ 1 }{ 1 + e^{-z} }$
この導関数 $\frac{ \partial a }{ \partial z }$ の結果をaを用いて表すとどうなるでしょうか？
スラスラ算出できるようにしましょう*5。
ちなみに、シグモイド関数はnumpyには実装されていないので自分で書く必要があります。

def sigmoid(x): a = 1 / 1 + np.exp(-x) return a

合成関数の微分(またの名を連鎖律)は、単回帰分析における重みの算出(最小二乗法)、からニューラルネットワークまで、あらゆるところで出てきます。超超頻出です。

これ以外にも色々ある気がしますが力尽きてきたので、また今後、追記する可能性ありです。

混乱しがちな行列表現の定義と英語表現

正則行列: regular matrix , non-singular matrix(非特異行列), inversible matrix (可逆行列)

逆行列をもつ行列のこと。 $AB = BA = E$
を満たすn次正方行列Bが存在するとき、BをAの逆行列といい、Aは正則であるという。
すごく覚えにくいが、英語でいろんな言い回しがされているので、わかるようにした方が良さそう。
私なりの覚え方↓
regular = 等辺等角 → 数学でいう正多角形の「正」の部分を表す
inversible = 逆にできる → 逆行列が存在する。
non-singular = 非特異値 → なんか0が多くなさそうだから逆行列持ちそう(適当)

転置行列: transpose

$A^{\mathrm{T}} = A$ となるような正方行列A

直交行列: orthogonal matrix

$A^{ \mathrm{T} }A = AA^{ \mathrm{T} } = E, すなわち A^{ \mathrm{T} } = A^{-1}$ となるような正方行列A

(補足) エルミート行列 $A^{\dagger}$ : hermitian matrix

定義は $A^{\dagger} = A$
ある行列Aの複素共役(複素部分の符号を反対にすればいい)をとり、さらに転置させた $A^{\dagger}$ が元の行列Aに等しいということ。
つまり、「対称行列」をさらに複素数の行列に対して一般化したもの。

(補足) ユニタリー行列 $A^{*}$ : unitary matrix

定義は $U^{*}U = 1$
これは、「直交行列」をさらに複素数の行列に対して一般化したもの。
以下定義省略で英単語リスト

逆行列: inverse matrix

対角行列: diagonal matrix

固有ベクトル/ 固有値: eigen vectors/ eigen values

最後に

深夜に思いつく限りのことを書き出しました*6。
私自身、機械学習という底無し沼にしばしば絶望感を覚えつつも、あ〜〜色々分かって繋がって楽し〜〜と思いながら勉強しています。楽しむのが一番です。
至らないところが多々ありますが、初心者視点の本記事が次に勉強する人たちの少しでも役に立てますように。
間違っている箇所があったら指摘していただけると幸いです。

参考文献

1. 奥村吉孝, 手嶋忠之(2012), 基礎から学び考える力をつける線形代数
2. 長畑秀和(2001), 多変量解析へのステップ
3. [第2版]達人データサイエンティストによる理論と実践 Python 機械学習プログラミング

*1:まだ全然好きじゃない

*2:特に研究室所属したての後輩とかに見てもらいたい…

*3:最近Courseraの大人気Andrew Ng先生のコースでニューラルネットワークを学んでいるが、深層学習の研究分野では各データが1列で表記されるのが一般的らしく、絶賛混乱している。ので、行と列が何を表しているのか常に意識するの超大事。

*4:参考文献1より

*5:a(1-a)になります

*6:めっちゃ時間かかった割に読み返してみるとあんまり内容がない......

wimper_1996 2020-01-23 14:17 読者になる

広告を非表示にする

もっと読む

コメントを書く

次のページ